Huffman压缩

数据结构 大作业一

一、问题描述

在合适的情况下，利⽤ Huffman 编码对⽂件进⾏压缩可以减少其占⽤空间，同时在需要使⽤到⽂件的 时候也可以根据压缩⽂件中所提供的信息来将其还原为原⽂件。本次实验中，我们将实现⼀个基于 Huffman 编码的⽂件压缩/解压缩⼯具。

二、基本要求

基于 Huffman 编码实现⼀个压缩器和解压缩器（其中 Huffman 编码以字节作为统计和编码的基本符号 单元），使其可以对任意的⽂件进⾏压缩和解压缩操作。针对编译⽣成的程序，要求压缩和解压缩部分 可以分别独⽴运⾏。具体要求为：

• 每次运⾏程序时，⽤⼾可以指定只压缩/只解压缩指定路径的⽂件。实现的时候不限制与⽤⼾的交 互⽅式，可供参考的⽅式包括但不限于
  • 根据命令⾏参数指定功能（压缩/解压缩）和输⼊/输出⽂件路径
  • GUI 界⾯
  • 运⾏程序后由⽤⼾交互输⼊指定功能和路径

• 【CAUTION!】不被允许的交互⽅式： 通过修改源代码指定功能和⽂件路径

• 压缩时不需要指定解压⽂件的⽬标路径，解压缩时不需要指定压缩前原⽂件的路径，压缩后的⽂件 可以换到另⼀个位置再做解压缩

三、程序能实现的功能

1. 压缩指定路径的任意格式的文件
2. 解压指定路径的文件(无损)
3. 可以选择压缩的基本单元(0.5Byte ~ 4Byte)
4. 可以选择使用多元 Huffman 数进行压缩 (2~16)
5. 3，4 项同时使用

四、实验思路

1. 压缩
   • 第一遍扫描文件，根据用户选择的压缩基本单元，统计每一种基本单元出现的频次
   • 以出现的频次作为权重，根据用户选择构建 Huffman 树，若用户选择多元压缩，则首先补全节点数，其次使用优先队列，每次弹出最小的元素，构造 Huffman 树
   • 根据构造出的 Huffman 树，求得 Huffman 编码 (压缩单元较小时，使用指针 new 内存的形式加速，压缩单元较大时，使用 map 来控制内存的使用)
   • 首先输出被压缩文件的类型，压缩时使用的基本单元大小，Huffman 树种类，再输出每一个基本单元出现的频次
   • 再次扫描文件，每当获取一个基本单元大小的字节，二进制输出它的 Huffman 编码 (每八位以一个字符的形式输出)
2. 解压
   • 首先获得压缩文件头部的相关信息，以及各个基本单元出现的频次
   • 用和压缩时完全相同的方式构造出 Huffman 树，获得 Huffman 编码
   • 扫描剩下的文件内容，根据二进制编码，转化为原来的基本单元输出

五、项目结构

─ huffman-compress
  ├── CMakeLists.txt
  ├── include
  │   ├── big.h
  │   ├── huffman.h
  │   ├── small.h
  │   └── tempwindow.h
  └── src
      ├── big.cpp
      ├── huffman.cpp
      ├── main.cpp
      ├── small.cpp
      └── tempwindow.cpp

六、关键内容实现

1. huffman树的建立

//初始化 huffman树
long long int fre = map.size();
HT = new HTNode[2 * fre];
for (long long int i = 0; i < 2 * fre; i++)
{
    HT[i].num = i;
    HT[i].key = 0;
    HT[i].weight = 0;
    for (int j = 0; j < tree_n; j++)
        HT[i].child[j] = 0;
    HT[i].parent = 0;
}
int index = 1;
HT[0].weight = INT_MAX;
for (auto iter : map)
{
    HT[index].key = iter.first;
    HT[index].weight = iter.second;
    index++;
}
//使用优先队列构造huffman树
std::priority_queue<HTNode> ans;
for (int i = 1; i <= fre; i++)
    ans.push(HT[i]);
if (tree_n != 2)
{
    int blank;
    if (fre % (tree_n - 1) == 0)
        blank = 1;
    else
        blank = tree_n - fre % (tree_n - 1);
    if (blank != tree_n - 1)
    {
        HuffmanTree Tree_blank = new HTNode;
        Tree_blank->key = 0;
        Tree_blank->parent = 0;
        Tree_blank->weight = 0;
        for (int j = 0; j < tree_n; j++)
            Tree_blank->child[j] = 0;
        for (int i = 0; i < blank; i++)
        {
            Tree_blank->num = fre + i + 1;
            ans.push(*Tree_blank);
        }
    }
}
//要从加了0之后开始计算 即修正fre
for (long long int now = fre + 1; now < 2 * fre; now++)
{
    int now_weight = 0;
    for (int i = 0; i < tree_n; i++)
    {
        HTNode temp_Node = ans.top();
        HT[temp_Node.num].parent = now;
        HT[now].child[i] = temp_Node.num;
        now_weight += temp_Node.weight;
        ans.pop();
    }
    HT[now].weight = now_weight;
    if (ans.empty())
        break;
    ans.push(HT[now]);
}

2. 获取huffman编码

char *cd = new char[fre];
cd[fre - 1] = '\0';
for (long long int i = 1; i <= fre; i++)
{
    long long int start = fre - 1;
    long long int j, p;
    for (j = i, p = HT[i].parent; p != 0; j = p, p = HT[p].parent)
    {
        int index = 0;
        while (HT[p].child[index] != j)
            index++;
        int wei = judge(tree_n);
        for (int i = 0; i <= wei - 1; i++)
            cd[--start] = ((index >> i) & 1) + '0';
    }
    HC[HT[i].key] = (char *)malloc((fre - start) * sizeof(char));
    strcpy(HC[HT[i].key], &cd[start]);
}

3. 压缩

while (infile.get(c))
{
    now_byte++;
    char_now = 0;
    while (char_now < 8)
    {
        while (char_now < 8)
        {
            tt_key += (((int)c >> (7 - char_now)) & 1) << (every - 1 - now_bit);
            char_now++;
            now_bit++;
            if (now_bit == every)
                break;
        }
        if (now_bit == every)
        {
            i = 0;
            while (HC[tt_key][i] != '\0')
            {
                tt += (HC[tt_key][i] - '0') << (7 - num);
                i++;
                num++;
                if (num == 8)
                {
                    outfile.put((char)tt);
                    num = 0;
                    tt = 0;
                }
            }
            now_bit = 0;
            tt_key = 0;
        }
    }
}
//输出最后一个可能没有到达一个单位的字符
if (now_bit != every && now_bit != 0)
{
    i = 0;
    while (HC[tt_key][i] != '\0')
    {
        tt += (HC[tt_key][i] - '0') << (7 - num);
        i++;
        num++;
        if (num == 8)
        {
            outfile.put((char)tt);
            num = 0;
            tt = 0;
        }
    }
}
//输出可能没有到达8bit的最后一个字符
if (num != 0)
    outfile.put((char)tt);

4. 解压

while (1)
{
    infile.get(c);
    int tt = c;
    index = 0;
    for (int i = 7; i >= 0; i--)
        ans[index++] = ((tt >> i) & 1) + '0';
    index = 0;
    while (1)
    {
        switch_child += (ans[index] - '0') << (wei - 1 - wei_now);
        wei_now++;
        if (wei == wei_now)
        {
            wei_now = 0;
            now = HT[now].child[switch_child];
            switch_child = 0;
        }
        index++;
        if (HT[now].child[0] == 0)
        {
            //获取对应权值对应的 bit位
            int int_to_char = HT[now].key;
            char ans_[every + 1];
            ans_[every] = '\0';
            for (int j = 0; j < every; j++)
                ans_[j] = ((int_to_char >> (every - 1 - j)) & 1) + '0';
            int j = 0;
            while (ans_[j] != '\0')
            {
                now_bit++;
                out_tmp += (ans_[j] - '0') << (8 - now_bit);
                if (now_bit == 8)
                {
                    char_size--;
                    outfile.put(out_tmp);
                    now_byte++;
                    tmp_struct = {now_byte, size};
                    out_tmp = 0;
                    now_bit = 0;
                }
                j++;
                if (char_size == 0)
                    break;
            }
            now = root_loc;
        }
        if (index == 8 || char_size == 0)
            break;
    }
    if (char_size == 0)
        break;
}

七、编译过程

• 编译环境

  • Ubuntu-20.04 ( wsl2 )
  • gcc 9.3.0
  • cmake version 3.16.3

• CMakeLists.txt (注意修改 Debug 模式和 Release 模式)

  cmake_minimum_required(VERSION 3.5)
  
  project(yasuo)
  
  set (CMAKE_CXX_STANDARD 17)
  
  set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -pthread" )
  
  set(SOURCES
      src/main.cpp
      src/big.cpp
      src/small.cpp
      src/tempwindow.cpp
      src/huffman.cpp)
  
  add_definitions(-w)# system忽略了返回值，消除编译警告
  
  add_executable(yasuo ${SOURCES})
  
  SET(CMAKE_BUILD_TYPE "Release")
  
  target_include_directories(yasuo
  PRIVATE
      ${CMAKE_CURRENT_SOURCE_DIR}/include)

• 编译操作(Release 版本为例，首先进入项目目录)

  mkdir Release
  cd Release
  cmake ..
  make
  ./yasuo
  # 运行程序

八、运行效果

• 使用 1.5Byte 为基本单元，三叉 Huffman 树压缩 png 文件，源文件 258kb，压缩后 182kb，解压后 258kb，效果较为明显，同时文件解压后无任何变化

  

• 性能测试

  使用该程序压缩大小 1.3G 的 txt 文档

  • 压缩用时：130.917s

  • 解压用时：113.172s

  • 压缩效率：$46\%$

    

九、关于 Huffman 压缩的探索

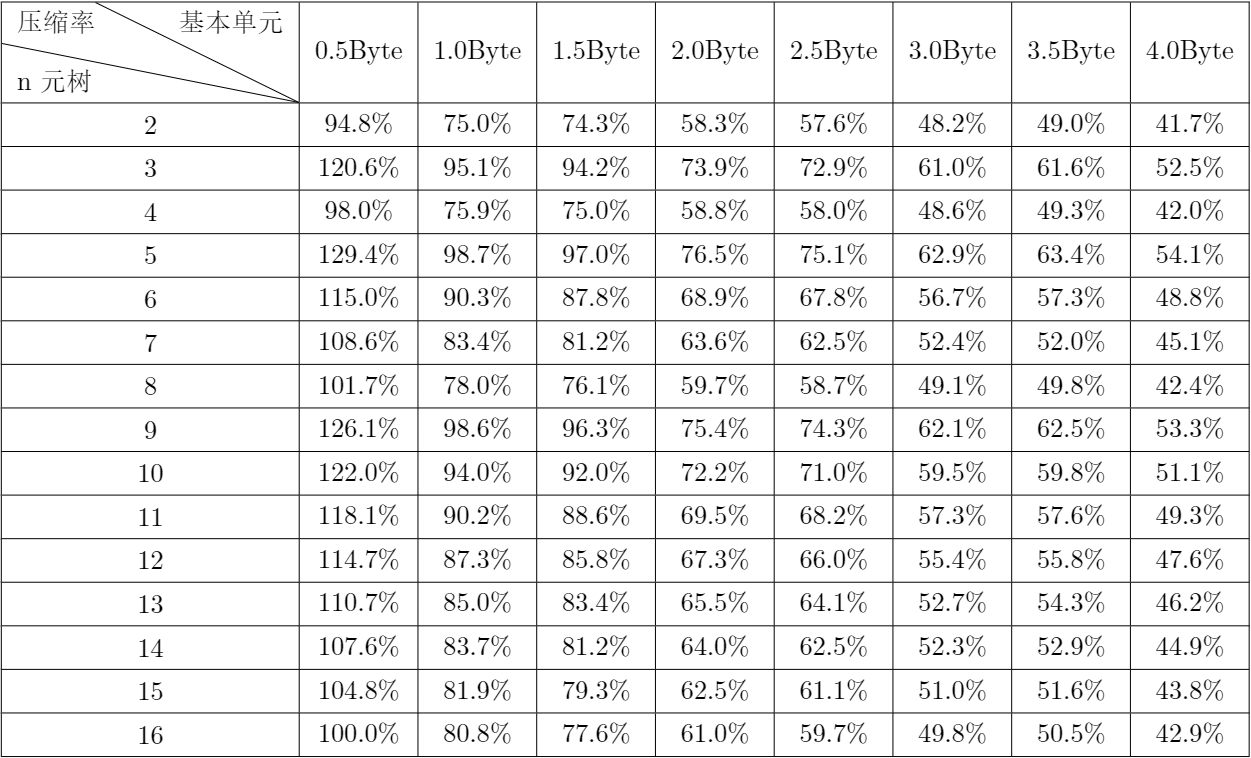
• 压缩一包含中英文及数字的 txt 文档，压缩效果如下(压缩率=$\frac{\text{压缩文件大小}}{\text{原始文件}}$)
  

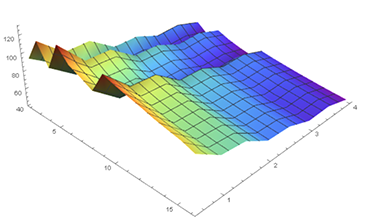
• 利用上述数据作图 (mathematica 作图有一定偏差)

  

• 根据上述实验数据可以看出:

  • 压缩基本单元为 0.5Byte 时，基本没有压缩效果
  • 随着压缩基本单元的增大，压缩效果总体上呈现上升趋势
  • 在压缩的基本单元从 3.0Byte 变为 3.5Byte 时，压缩效果均有小幅下降
  • 当选用$2^n$叉 Huffman 树时，压缩效果明显更佳，而当选用$2^n+1$叉 Huffman 树时，压缩效果较差 ($2^n$叉 Huffman 树每一个节点都刚好可以利用 $n$ bit 的 Huffman 编码)
    因此，在压缩 txt 文本文件时，选用$2^n$叉 Huffman 树，在综合时间的情况下选择更大的压缩基本单元，能够提高压缩效率

    同时值得指出的是，对于图片，视频等文件类型，基本单元极有可能发生出现次数相近的情况，此时综合时间等考虑，可以尽量选择 1Byte 为压缩的基本单元

十、源码

    戳这里