Dijkstra实现导航软件

数据结构 大作业二

一、实验要求

    要求在所给的数据集上建立图结构（邻接矩阵或者邻接表），并在建立的图结构上自行实现Dijkstra算 法求解任 意两点之间的最短路径。

• 输入输出要求：
  Input : src(源点) Dst(目标点)
  Output :
      (1) 最短路径的长度： distance
      (2) Src到Dsr的一条最短路径，例如：Src->p1->p2->p3->…->Dst(逆序输出也对)

二、实验目的，

    熟悉并掌握图的建立算法和Dijkstra求图上最短路径算法，了解Dijkstra算法的改进方法，掌握时间复杂度的分析方法并且去分析对比验证不同时间复杂度的Dijkstra算法的时间开销，了解稀疏的图结构的压缩存储方法。

三、程序能实现的功能

• 对数据文件进行二进制处理，同时少量压缩二进制文件
• 根据数据文件建立图结构(邻接表)
• 使用朴素法，二叉堆，配对堆，fibonacii堆搜索最短路径，对于大数据测试样例，搜索时间能够sub10

四、设计思路

• 预处理
  • 将原数据文件转换为二进制形式
  • 建立图的邻接表，将图按顺序输出，同一个出发点的边只记录以此源点，用度数来标记下一个源点
• dijkstra
  • 建立visited与distance数组
  • 初始visited数组置0，distance数组置最大(由于memset()的限制，稍小于INT_MAX)
  • 将源点距离设为0，访问设为1，遍历所有与源点相连的边，记录距离进入distance数组
  • 从distance数组中找出distance最短的点，记为$u$，遍历所有与$u$相连的边，相连的点记为$v_1,v_2,...,v_n$，如果$visited[v_i]==0\& distance[v_i]>distance[u]+weight_{u->v}$，更新$distance[v_i]$的值
  • 重复上述操作，知道$visited[Dst]==1$或者整个图已搜索完毕，仍然没有找到路径
  • 逆序输出最短路径

五、项目结构

─ navigation
  ├── binary
  │   └── pre.cpp
  ├── CMakeLists.txt
  ├── include
  │   ├── dijkstra.h
  │   ├── fibheap.h
  │   ├── graph.h
  │   ├── Heap.h
  │   └── pair_heap.h
  └── src
      ├── dijkstra.cpp
      ├── fibheap.cpp
      ├── graph.cpp
      ├── Heap.cpp
      ├── main.cpp
      └── pair_heap.cpp

六、关键内容实现

1. dijkstra(堆优化)

int *visited = new int[100000000];
memset(visited, 0, sizeof(int) * 100000000);
int *dis = new int[100000000];
memset(dis, 127, sizeof(int) * 100000000);
int *pre = new int[100000000];
memset(pre, -1, sizeof(int) * 100000000);
Heap<struct node> q;
dis[x] = 0;
q.push(node(x, dis[x]));
while (!q.empty())
{
    struct node now = q.top();
    q.pop();
    if (visited[now.begin] == 1)
        continue;
    visited[now.begin] = 1;
    if (now.begin == y)
        break;
    struct ArcNode *p = G.data[now.begin]->firstarc;
    while (p != nullptr)
    {
        if (visited[p->adjvex] != 1 && dis[p->adjvex] > dis[now.begin] + p->weight)
        {
            dis[p->adjvex] = dis[now.begin] + p->weight;
            q.push(node(p->adjvex, dis[p->adjvex]));
            pre[p->adjvex] = now.begin;
        }
        p = p->nextarc;
    }
}
if (visited[y] != 1)
{
    std::cout << "不能到达!" << std::endl;
    delete[] visited;
    delete[] dis;
    delete[] pre;
    return;
}
int road = y;
while (road != -1)
{
    printf("\033[0;30;47m%d\033[0m ", road);
    road = pre[road];
    if (road != -1)
        std::cout << "<- ";
    else
        printf("\n");
}
std::cout << "\nOutput:\n"
          << dis[y] << std::endl;

delete[] visited;
delete[] dis;
delete[] pre;

2. 二叉堆

• 存储结构

  template <class T>
  class Heap
  {
  private:
      std::vector<T> data;
      int length;
  
  public:
      Heap();
      ~Heap();
      inline void swim(int k);      //上浮
      inline void sink(int k);      //下沉
      inline void push(T e);        //入堆
      inline void pop();            //出堆
      inline T top();               //返回堆顶元素
      inline bool empty();          //判断是否为空
      inline int size();            //返回大小
      inline void swap(T &a, T &b); //交换元素
  };

• 上浮

  while (k > 1 && data[k] > data[k / 2])
  {
      swap(data[k], data[k / 2]);
      k /= 2;
  }

• 下沉

  while (k * 2 <= length)
  {
      int j = 2 * k;
      if (j < length && (data[j] < data[j + 1])) //找到左右子树中更小的
          j++;
      if (data[k] > data[j])
          break;
      swap(data[k], data[j]);
      k = j;
  }

3. 配对堆

• 存储结构

  template <class T>
  class pair_node
  {
  public:
      T val;
      int left;
      int right;
      pair_node()
      {
          left = 0;
          right = 0;
      }
      pair_node(T e)
      {
          val = e;
          left = 0;
          right = 0;
      }
  };
  template <class T>
  class pair_heap
  {
  private:
      std::vector<pair_node<T>> data;
      int length; //已经到达的vector地址
      int _size;  //实际存储的大小
      inline void merge(int x, int y);
      inline int merges(int x, int y);
      int root;
      inline int pop_();
  
  public:
      pair_heap();
      ~pair_heap();
      inline void push(T e);
      inline void pop();
      inline void _pop();
      inline T top();
      inline bool empty();
      inline int size();
  };

• merge

  void merge(int x, int y)
  {
      if (!x || !y)
          root = x + y;
      else if (x == y)
          root = x;
      else
      {
          if (data[x].val < data[y].val)
          {
              int temp = x;
              x = y;
              y = temp;
          }
          data[y].right = data[x].left;
          data[x].left = y;
          data[x].right = 0;
          root = x;
      }
  }

• pop即反复merge根节点的孩子节点

4. Fibonacii堆

• 存储结构

  template <typename T>
  struct fib_node
  {
      struct fib_node<T> *parent;
      struct fib_node<T> *child;
      struct fib_node<T> *left;
      struct fib_node<T> *right;
      T key;
      int degree;
      fib_node() : parent(nullptr), child(nullptr), left(this), right(this), degree(0) {}
  };
  template <class T>
  class FibHeap
  {
  private:
      int keyNum;
      int maxDegree;
      struct fib_node<T> *min;
      struct fib_node<T> **cons;
      void removeNode(struct fib_node<T> *node);
      void addNode(struct fib_node<T> *node, struct fib_node<T> *root);
      void consolidate();
      struct fib_node<T> *extractMin();
      void makeCons();
      void link(struct fib_node<T> *node, struct fib_node<T> *root);
      void theEnd(struct fib_node<T> *node);
  
  public:
      FibHeap();
      ~FibHeap();
      void push(T e);
      void pop();
      bool empty();
      int size();
      T top();
  };

• 具体操作见源码

七、测试程序的正确性及性能

引入pbds库中各种最小堆进行比较

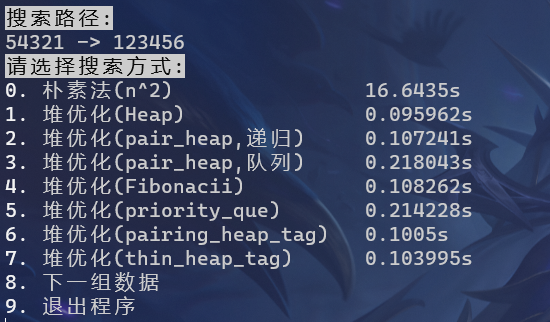
• 对于小数据测试样例

  

  可以看到，对于小数据测试样例，除了朴素法时间过长以外，手写的堆以及pbds库中的堆都可以在1s之内完成搜索，由于电脑性能不稳定，时间的差距可以忽略

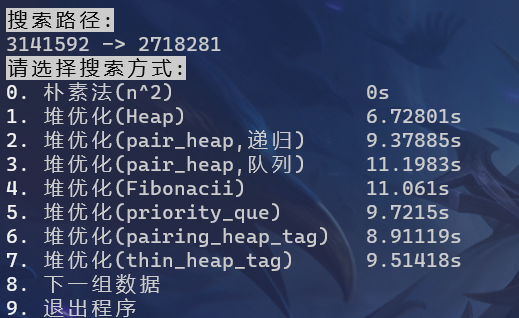
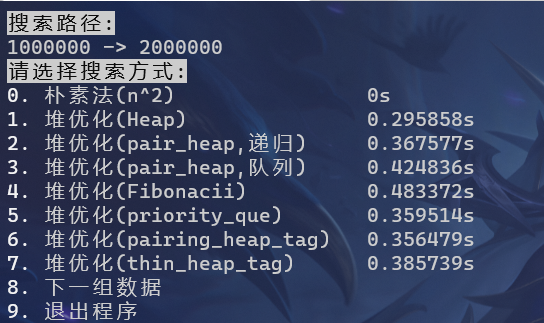
• 对于两组大数据测试样例

  • 3141592->2718281

  

  • 1000000->2000000

  

  • 对于大数据测试，朴素法在一个小时内都无法搜索出答案

  • 所有堆优化的算法都可以在25s之内完成搜索

  • 手动实现的二叉堆拥有最好的性能，较之系统的优先队列，也有更好的表现

  • 递归实现pop的配对堆与系统配对堆性能相仿，队列实现pop则稍有差距(如果在编译时开启O2优化，队列的性能会强于递归，但是O2优化不够稳定)

  • Fibonacci堆较之pbds库有着不小的差距

• 一些思考

  配对堆和Fibonacci堆在理论上的时间复杂度都应该优于二叉堆，但是手写的二叉堆反而性能最佳，pbds库配对堆和Fibonacci堆较二叉堆也没有极其突出的表现，我认为原因可能有：

  • 测试数据点特殊，具有偶然性
  • 在入堆的操作上，二叉堆是$O(log(n))$的，配对堆和Fibonacci堆是$O(1)$的，此时二叉堆的性能较差，但由于数据特殊性，在每次入堆时，所需要经历的上浮操作较少
  • 在出堆的操作上，三种堆结构均是$O(log(n))$的，但是配对堆和Fiboncci堆是均摊复杂度，单次操作极限情况下:$\lim_{n\to+\infty}\frac{n}{2}+\frac{n}{4}+\frac{n}{8}+...=n$，由于出堆几乎不是连续的，虽然上次出堆使根节点的孩子节点变成了原来的一半，由于不能立刻弹出，经历了多次入堆操作后，出堆的复杂度仍然是较高的，浪费了过多的时间

八、编译过程

• 编译环境

  • Ubuntu-20.04 ( wsl2 )
  • gcc 9.3.0
  • cmake version 3.16.3

• CMakeLists.txt (注意修改Debug模式和Release模式)

  cmake_minimum_required(VERSION 3.5)
  
  project(navigation)
  
  set (CMAKE_CXX_STANDARD 17)
  
  set(SOURCES
      src/main.cpp
      src/dijkstra.cpp
      src/graph.cpp
      src/Heap.cpp
      src/pair_heap.cpp
      src/fibheap.cpp)
  
  add_executable(navigation ${SOURCES})
  
  SET(CMAKE_BUILD_TYPE "Release")
  # SET(CMAKE_BUILD_TYPE "Debug")
  
  target_include_directories(navigation
  PRIVATE
      ${CMAKE_CURRENT_SOURCE_DIR}/include)

• 编译操作(Release版本为例，首先进入项目目录)

  mkdir Release
  cd Release
  cmake ..
  make
  ulimit -s unlimited # linux下打开内存限制
  ./navigation
  # 运行程序

九、源码

    戳这里